Ressources
- DNA
To simplify our study, we will consider that a DNA sample is made up of 6 characters using only the letters A and B, for example:
sequence AAAAAA
sequence ABABAA
With these 6 characters, each having only two possible values (A or B), we obtain 64 different combinations.
Among the pieces of evidence available to you, you may have sequences composed of these 6 characters.
Щоб спростити наше дослідження, ми будемо вважати, що зразок ДНК складається з 6 символів, утворених лише літерами A та B, наприклад:
послідовність AAAAAA
послідовність ABABAA
Оскільки кожен із цих 6 символів може мати лише два значення — A або B — ми отримаємо 64 різні комбінації.
Серед доказів, які є у вашому розпорядженні, можуть бути послідовності, що складаються з цих 6 символів.
Pour simplifier notre étude on va considérer qu'un échantillon d'ADN est constituée de 6 caractères constituées avec les lettres A et B, par exemple:
séquence AAAAAA
séquence ABABAA
Avec ces 6 caractères chacun n'ayant que deux valeurs possibles A ou B , on obtiendra 64 combinaisons différentes.
Sur les preuves à votre disposition vous avez peut être des séquences composées de ces 6 caractères
- SOUND
This chapter introduces a few basic concepts about sound. You are not required to understand everything, but certain ideas—such as frequency or the harmonics of a sound—are important for the labwork.
Sound is a wave produced by a vibration (vocal cords, etc.). It propagates thanks to the elasticity of the medium it travels through. The auditory sensation is the interpretation of this sound by our ears.
У цьому розділі подано кілька основних понять про звук. Вам не обов’язково все розуміти, але деякі поняття — такі як частота або гармоніки звуку — є важливими для виконання завдання.
Звук — це хвиля, що виникає внаслідок вібрації (голосові зв’язки тощо). Він поширюється завдяки пружності середовища, через яке проходить. Слухове відчуття — це інтерпретація звуку нашими вухами.
Ce chapitre vous présente quelques notions sur le son. Vous n'êtes pas obligé de tout comprendre mais certaines notions comme la fréquence ou les harmoniques d'un son sont importantes pour l'activité.
Le son est une onde produite par une vibration ( corde vocale, etc.), il se propage grâce à l'élasticité du milieu traversé. La sensation auditive est l'interprétation du son par nos oreilles.
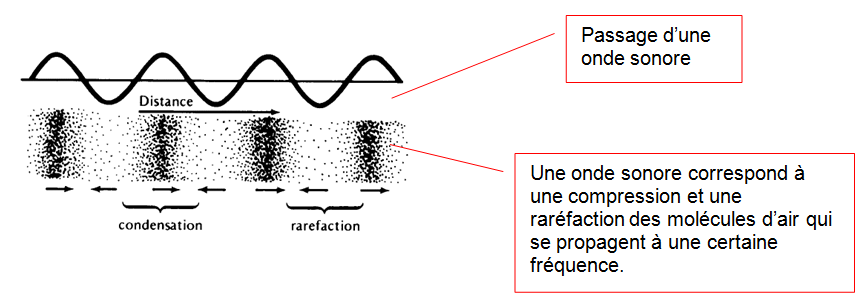
There are several ways to describe sound. The approaches depend on the type of sound being described (pure sound, complex sound) and on the field of study (such as physics or music).
Існує кілька способів описати звук. Підходи залежать від типу звуку, який потрібно описати (чистий звук, складний звук), а також від сфери діяльності (наприклад, фізика або музика).
Il y a plusieurs façons de décrire le son. Les approches dépendent du type de son à décrire ( son pur, son complexe) et du domaine d'activité ( la physique ou la musique par exemple)
- PURE SOUND
A pure sound is made up of a sinusoidal sound wave.
Чистий звук складається з синусоїдальної звукової хвилі.
Un son pur est constitué d'une onde sonore sinusoïdale.
Physics approach
A sinusoidal wave can be described by its amplitude and its period:
Синусоїдальну хвилю можна описати її амплітудою та періодом:
Une onde sinusoïdale peut se décrire par son amplitude et sa période:
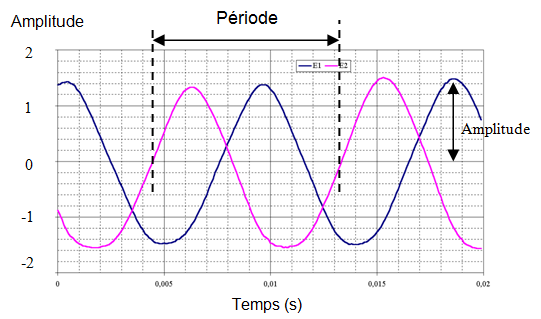
- PERIOD AND FREQUENCY
The period T (s) corresponds to the time the wave takes to return to a previous identical state (Period ⇔ the time separating two identical phases of air‑molecule compression at a point through which the wave passes).
The frequency F (Hz) is often preferred over the period to describe a sound. Frequency corresponds to the number of periods the wave produces in one second. Frequency affects how we perceive sound. We can hear a sound only if the wave has a frequency between 20 Hz and 20,000 Hz.
Knowing the period T in seconds, the frequency F in Hertz is calculated using the formula:
F (Hz) = 1 ÷ T (s)
1 Hertz ⇔ 1 period per second
- La période T (s) correspond au temps que met l'onde pour retrouver un même état précédent ( Période <=> temps séparant deux phases de compression identiques des molécules d'air en un point où passe l'onde).
- La fréquence F (Hz) est souvent préférée à la période pour décrire un son. La fréquence correspond au nombre de périodes que l'onde produit en un temps égal à une seconde. La fréquence à une incidence sur notre perception du son. Nous entendons un son que si l'onde a une fréquence comprise entre 20 Hz et 20 000 Hz.
Connaissant la période T en secondes, on calcule la fréquence F en Hertz avec la formule : F(Hz) = 1 ÷T(s)
1Hertz <=> 1 période par seconde
- Amplitude of a sound wave
The amplitude of a sound wave is measured in Pascals (Pa). It represents the variation in pressure produced by the wave as it travels (this pressure is called acoustic pressure ⇔ the force exerted by air molecules on a surface when the sound wave passes). The amplitude of the wave at a given moment is called the instantaneous acoustic pressure.
Since the wave is sinusoidal, the acoustic pressure at a point increases above atmospheric pressure during the compression phase of the air molecules, reaches a maximum, then decreases during the rarefaction phase. This phenomenon repeats identically with a period T as long as the source of the wave continues without attenuation.
Calculating acoustic pressure is complex and goes beyond the scope of high‑school activities.
Instead of acoustic pressure, physicists use the sound level (in English: Sound Pressure Level, SPL), calculated or measured in decibels (dB).
The sound level at a point A involves the ratio between the acoustic pressure at point A and a reference acoustic pressure equal to 20 μPa (20 μPa is the lowest acoustic pressure the human ear can perceive).
Although calculating the sound level, noted Lp, is difficult, measuring it is easy using a sound level meter; one simply needs to know how to interpret the values displayed in dB.
L'amplitude d'une onde sonore se mesure en Pascal (Pa), elle représente la variation de pression que produit l'onde où elle passe ( la pression est ici dite acoustique <=> force qu'exerce les molécules d'air sur une surface lorsque l'onde sonore passe). L'amplitude de l'onde à un instant donné est appelée la pression acoustique instantanée. L'onde étant sinusoïdale, la pression acoustique en un point croit par rapport à la pression atmosphérique durant la phase de compression des molécules d'air, passe par un maximum, puis décroit durant la phase de raréfaction des molécules d'air, le phénomène se répète à l'identique avec une période T tant que la source de l'onde existe sans atténuation. Calculer la pression acoustique reste complexe et sort du cadre des activités d'un élève de lycée.
Plutôt que la pression acoustique, les physiciens utilisent le niveau sonore ( en Anglais Sound Pressure level: SPL) calculé ou mesuré en décibels (dB). Le niveau sonore en un point A fait intervenir le rapport entre la pression acoustique au point A et une pression acoustique de référence égale à 20 μPa ( 20 μPa est le niveau le plus faible de pression acoustique que l'oreille puisse percevoir). Le calcul du niveau sonore noté Lp est difficile par contre on peut mesurer facilement le niveau sonore avec un sonomètre; il suffit juste de savoir interpréter les valeurs affichées en dB.
Musical approach
The way sound is described in music is far too broad a topic to be fully covered in this introduction to sound. We will simply mention the relationship between musical notes and their frequency, as well as the notion of timbre, which allows us to identify a voice or a musical instrument. These concepts are important for a sound engineer (or for forensic acoustics).
La manière de décrire les sons en musique est un sujet trop vaste pour être abordé de manière complète dans cette introduction aux sons. On citera juste la relation entre les notes de musique et leur fréquence ainsi que la notion de timbre qui permet d'identifier une voix ou un instrument de musique; ces grandeurs sont importantes pour un ingénieur du son (ou pour la police scientifique).
- Pitch
When the human ear detects a sound, the brain extracts its pitch (whether the sound is high or low).
In music, pitch is indicated by the name of a note on a scale. The difference in pitch between two notes is called an interval. The same note repeats at each octave.
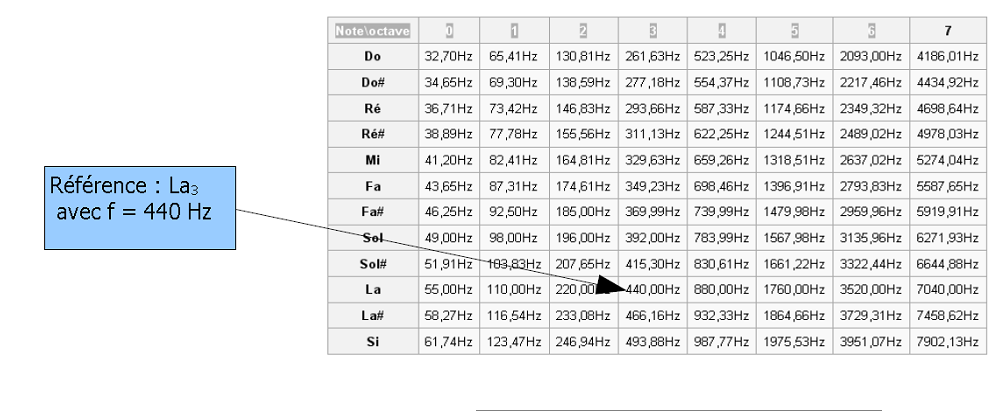
The table below gives the frequency values of musical notes:
Lorsque l’oreille humaine capte un son, le cerveau en extrait la hauteur (le son est aigu ou grave).
En musique, on désigne la hauteur par le nom d'une note sur une échelle ou une gamme. On appelle intervalle l'écart de hauteur entre deux notes. Une même note se répète à chaque octave.
Le tableau ci-après donne la valeur des fréquences des Notes de musique:
- Timber and complex sound
The timbre of an instrument or a voice corresponds to its musical identity. If the same note is played on two different instruments, the auditory sensation is not the same because the two instruments do not have the same timbre.
When we analyze a note produced by an instrument, we realize that it is not a pure sound (a sinusoidal wave) but a complex sound (a wave with a non‑sinusoidal shape).
Here is the time‑domain waveform of the sound corresponding to the note A3 displayed with the Audacity software; you can see that it is not a sinusoidal wave:
Le timbre d’un instrument ou d'une voix correspond à son identité musicale. Si une même note est jouée sur deux instruments différents, la sensation sonore n'est pas la même parce que les deux instruments n'ont pas le même timbre.
Lorsque l'on analyse une note produite par un instrument, on se rend compte que ce n'est pas un son pur ( une onde sinusoïdale) mais
un son complexe ( une onde de forme non sinusoïdale). Voici l'allure temporelle de l'onde sonore correspondant à la note La3 affichée avec le logiciel Audacity, vous pouvez voir que ce n'est pas une onde sinusoïdale:
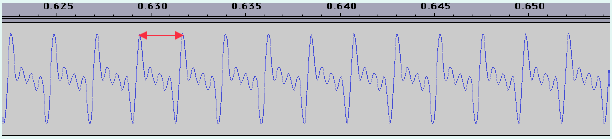
The physicist Joseph Fourier demonstrated that a complex sound (such as a note played by an instrument) can be considered as the sum of a set of sinusoidal waves of different frequencies (a set of pure tones with different frequencies).
A note produced by an instrument is the sum of a pure tone with a dominant frequency called the fundamental frequency, and other pure tones whose frequencies are multiples of this fundamental frequency (twice, three times, etc.). These are called harmonic frequencies.
The harmonic frequencies differ from one instrument to another, which is why the auditory sensation changes even when the same note is played on different instruments; we say that the instruments do not have the same timbre. The same applies to the human voice.
There is a measuring device called a spectrum analyzer, which displays the amplitudes and frequencies of the pure tones that make up a complex sound. Below is the note A3
Le physicien Joseph Fourier a démontré qu’un son complexe (tel qu’une note jouée par un instrument) pouvait être considéré comme l'addition d'un ensemble d'ondes sinusoïdales de fréquences différentes (un ensemble de sons purs de fréquences différentes).
Une note produite par un instrument est l'addition d’un son pur de fréquence dominante appelée la fréquence fondamentale et d'autres sons purs de fréquences multiples de cette fréquence fondamentale (le double, le triple, etc...) qui sont appelées les fréquences harmoniques. Les fréquences harmoniques sont différentes selon les instruments, c'est pourquoi la sensation sonore est différente si on joue la même note sur des instruments différents; on dit que les instruments n'ont pas le même timbre. Il en est de même pour la voix.
Il existe un appareil de mesure appelé analyseur de spectre qui affiche les amplitudes et les fréquences des sons purs qui composent un son complexe. Ci dessous, voici la note La3 jouée avec un instrument et sa restitution par un analyseur de spectre:
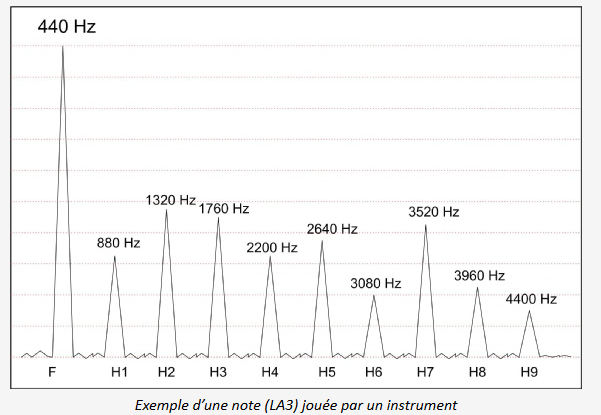
The graphical analysis shows that the note being played is A3, based on the value of the fundamental frequency of the sound, which is 440 Hz.
You can notice that the height of the line corresponding to the fundamental frequency is greater than that of the harmonic frequencies; it is the dominant frequency of the sound. The height of the lines represents the amplitude of each pure tone that makes up this complex sound, so the acoustic pressure of the fundamental is greater than that of the harmonics.
The harmonic frequencies are multiples of the fundamental frequency: harmonic 1 corresponds to 2 × the fundamental frequency, i.e., 880 Hz; harmonic 2 corresponds to 3 × the fundamental frequency, i.e., 1320 Hz; and so on.

L’analyse graphique révèle que la note jouée est La3 par la valeur de la fréquence fondamentale du son qui est 440 Hz.
Vous pouvez remarquer que la hauteur de la raie de la fréquence fondamentale est plus importante que celle des fréquences harmoniques, c'est la fréquence dominante du son . La hauteur des raies représente l'amplitude de chaque son pur qui compose ce son complexe, la pression acoustique du fondamental est donc plus importante que celle des harmoniques.
Les fréquences harmoniques sont des multiples de la fréquence fondamentale: l’harmonique 1 correspond à 2x la fréquence fondamentale soit 880 Hz, l’harmonique 2 correspond à 3x la fréquence fondamentale soit 1320 Hz, etc..
- Représentation temporelle et l'analyse spectrale
Exemple d'un son pur:
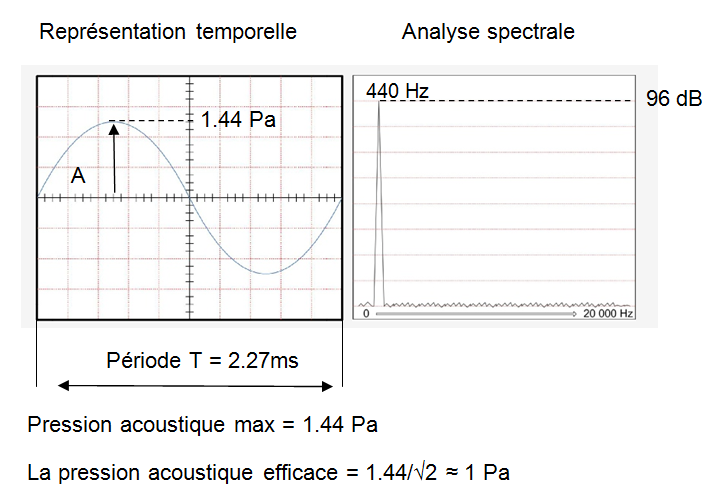
L'analyseur donne :
Le niveau sonore ( niveau de pression acoustique): 20 log ( 1/ 20.10-6) = 96 dB
La fréquence = 1/T = 1/ ( 2.27.10-3) ≈ 440 Hz
Pour aller plus loin
- interprétation du niveau sonore (dB-SPL)
Beaucoup de grandeurs en physique s'expriment en dB, pour les différentier on ajoute souvent un suffixe. Malheureusement beaucoup de fabricants, d'appareils ou de logiciels affichent des données en dB sans le suffixe; il convient alors de connaître la signification de la mesure pour pouvoir exploiter correctement les résultats.
Le niveau sonore se mesure en dB souvent suivi du suffixe SPL pour sound pressure level.
Une pression acoustique efficace de 20 µPa donnera un niveau sonore Lp= 0dB-SPL ( c'est le niveau minimum que l'on peut percevoir).
Une augmentation du niveau sonore de 1 dB-SPL correspondra à une augmentation de 12% de la pression acoustique.
Exemple une pression acoustique de Peff = 1 Pa donne Lp= 94 dB-SPL, si la pression augmente de 12% alors Peff = 1,12 Pa et le niveau sonore devient Lp= 95 dB-SPL.
Un niveau sonore Lp= 120 dB-SPL est considéré comme le seuil de douleur.
- Les dB acoustique (dBA)
On parle parfois de dBA, Il s'agit d'une pondération permettant la mesure du niveau sonore selon la sensibilité de notre oreille qui est différente suivant la fréquence.
L'oreille est un organe extrêmement sensible ! Il perçoit des pressions acoustiques variant de 2.10-5 Pa à 20 Pa
- Puissance acoustique (W et db-W)
La puissance acoustique en Watts est une valeur caractéristique des sources sonores (haut parleur, etc..), elle exprime l’énergie qui est échangée chaque seconde avec l'environnement. Pour une puissance acoustique donnée, le niveau sonore (la pression acoustique) dans le local va dépendre du milieu qui entoure la source et de la position du point de mesure. Plus on s'éloigne de la source sonore, plus la pression acoustique décroît. Le niveau sonore va dépendre également des qualités d'absorption des parois.
On peut établir une analogie avec l'éclairage : une lampe possède une puissance et son niveau d'éclairement dépend de la distance à laquelle on se trouve de la lampe et du local. Le niveau d'éclairement est l'équivalent de la pression acoustique pour la lumière, il est plus élevé dans une pièce dont les murs sont blancs ( les murs sont réfléchissants) que lorsque les murs sont sombres (les murs sont absorbants).
Le niveau de puissance sonore noté Lw est aussi exprimé en dB, il n'a rien à voir avec le dB-SPL. Il exprime un rapport de puissance entre la puissance de la source sonore ( haut parleur, etc..) et une valeur de référence de 10-12W.
- L'intensité acoustique (W/m2)
L’intensité acoustique est la puissance transportée par les ondes sonores dans une direction donnée, par unité de surface perpendiculairement à cette direction. Dit autrement on tient compte de la surface qui reçoit la puissance de l'onde sonore émise par la source. L'intensité acoustique représente le transfert de puissance sonore que réalise une onde sonore. S'il n'y a pas d'intensité acoustique, il n'y a pas de transfert d'énergie d'un endroit à un autre et donc pas de son. Au fur et à mesure que l'onde s'éloigne de la source, cette puissance totale se répartit sur une surface croissante. Dans les conditions de champ libre ( pas d'obstacle), l'intensité acoustique est proportionnelle au carré de la pression acoustique. Quand la distance à la source se multiplie par deux, la pression se divise par deux et l'intensité acoustique, proportionnelle au carré de la pression, se divise par quatre.
Le langage Nyquist
Audacity possède un langage appelé le langage Nyquist qui va vous permettre d'annuler le cryptage.
Le langage Nyquist est conçu pour travailler sur des sons, il possède de nombreuses fonctions qui manipulent les données audio.
Dans Audacity, il est ainsi aisé de construire des effets à partir des fonctions de base de Nyquist.
Pour accéder à la console de programmation Nyquist dans Audacity, il faut cliquer sur Effets -> Console Nyquist.
La zone sélectionnée sera placée dans la variable s et sera remplacée par le résultat de l'expression Nyquist que vous avez saisi.
Exemple: les fonctions suivantes créent de nouveaux sons :
- (hzosc 1000 ) Génère un son pur à la fréquence en 1000 Hz.
Les fonctions suivantes créent des combinaisons de sons :
- mult Multiplie deux sons
- add Additionne deux sons
Exemple:
(add s (hzosc 100)) : additionne le signal son s ( la zone sélectionnée de la piste son ) avec un signal sinusoïdal généré de fréquence 100Hz.
Le résultat de l'opération remplace la zone sélectionnée. Si la zone sélectionnée est toute la bande son, tout sera remplacé par l'opération.
Créé avec HelpNDoc Personal Edition: Générateur complet de livres électroniques ePub