Arbres binaires
Partie 1: description et parcours d'un arbre
On vous donne l'arbre suivant:
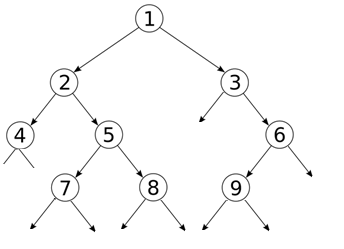
figure1
Question 1.1
Quelle est la taille de cet arbre? Quel est sa hauteur h si la racine est de profondeur 1?
Citer le nombre de feuilles de cet arbre.
Cet arbre est-il parfait?
Quelle est la profondeur du nœud 5?
Compte tenu de la hauteur h de l'arbre, quel est le nombre maximal N de nœuds qu'aurait pu avoir cette arbre? Exprimer la relation entre h et N
Question 1.2
On décide de coder cet arbre à partir d'objets nœuds décrits dans la classe suivante:
class Nœud:
def __init__(self, g,v,d):
self.gauche = g
self.valeur = v
self.droite = d
Coder l'arbre de la figure 1 à partir d'objets nœuds.
Question 1.3
Ecrire les fonctions python calcule_taille(arbre) et mesure_hauteur(arbre) qui permettent de déterminer la taille et la hauteur d'un arbre binaire. Vérifier que vous obtenez bien les mêmes valeurs qu'à la question 1.1
A) Parcours en profondeur infixe: Dans un parcours en profondeur infixe, on liste chaque nœud ayant un fils à gauche la seconde fois qu’on le voit et chaque nœud sans fils à gauche la première fois qu’on le voit, on commence par parcourir le sous-arbre de gauche. Les numéros sur les segments de l'arbre ci-dessous vous montre le sens parcours: la valeur 4 (sans fils à gauche) est affichée la première fois qu'elle est rencontrée soit à l'étape 2 du parcours, la valeur 2 qui a un fils à gauche sera affichée, la seconde fois qu'on le parcourt, au retour de l'étape 2 soit à l'étape 3. Pour l'arbre ci-dessous, on obtiendra l'ordre d'affichage: 427581396
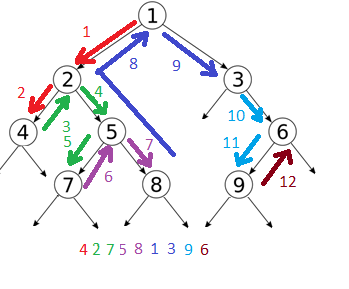
figure 2
On vous donne le programme python qui réalise ce parcours:
def parcours_infixe(arbre):
if arbre is None:
return
parcours_infixe(arbre.gauche)
print(arbre.valeur, end =";")
parcours_infixe(arbre.droite)
Question 1.4
Tester le code du parcours infixe sur l'arbre de la figure 1 et comparer avec les valeurs sous la figure 2.
Que se passe-t-il après un return suite à un test évalué True de if arbre is None ?
B) Parcours en profondeur préfixe: dans ce cas de parcours en profondeur, on liste chaque sommet la première fois qu’on le rencontre dans le parcours. Cela donne l'affichage: 124578369 pour l'arbre étudié.
pseudo code:
ParcoursPréfixe(arbre_binaire):
si arbre_binaire est vide:
retourner
Afficher valeur
ParcoursPréfixe( sous arbre_binaire gauche)
ParcoursPréfixe( sous arbre_binaire droit)
Question 1.5
Coder en python le pseudo code du parcours préfixe et tester le code.
C) Parcours en profondeur postfixe: dans ce cas de parcours en profondeur, on liste chaque sommet la dernière fois qu’on le rencontre. Cela donne l'affichage: 478529631 pour l'arbre étudié.
ParcoursPostfixe(arbre_binaire):
si arbre_binaire est vide:
retourner
ParcoursPostfixe( sous arbre_binaire gauche)
ParcoursPostfixe( sous arbre_binaire droit)
Afficher valeur
Question 1.6
Coder en python le pseudo code du parcours postfixe et tester le code.
C) Parcours en largeur: Le parcours d’un arbre en largeur consiste à partir de la racine puis visiter le fils gauche puis le fils droit, puis le fils gauche du fils gauche, puis le fils droit du fils droit, puis leurs enfants, etc.. Cela donne l'affichage: 123456789 pour l'arbre étudié.
On utilise une File f passée en paramètre de la fonction de parcours.
On passe également en paramètre de la fonction l’arbre à parcourir.
On met l’arbre à parcourir dans la file f.
Tant que la file n’est pas vide:
On enlève un element de la file
Si l'élément enlevé ne vaut pas None
On affiche la valeur du nœud de l'élément
On met dans la file son fils gauche
On met dans la file son fils droit
Question 1.7
Compléter le code ci-dessous pour le rendre conforme à l'algorithme ci-dessus. Détailler les étapes d'exécution de la fonction parcours_en_largeur(..) en précisant l'évolution de la file f ce qui vous permettra de comprendre le code de la fonction.
# la fonction de parcours en largeur
def parcours_en_largeur(un_arbre:object, f:list):
''' la fonction parcours en largeur un_arbre en utilisant une file f implémentée
avec une liste '''
# ajout de l'arbre dans la file
.............................
# tant que la file n'est pas vide
while .......:
# retrait de l'élément en tête de file
arbre = f.pop(0)
if arbre is not None:
# affichage de la valeur du nœud de arbre
print(.............., end= ";")
f.append(arbre.gauche)
# ajout de la branche droite de l'arbre dans la file
................................
# le programme principal
mon_arbre = Noeud( Noeud( Noeud( None,4, None) ,2, Noeud( Noeud( None,7, None) ,5, Noeud( None,8, None))), 1 , Noeud( None,3, Noeud( Noeud( None,9, None),6, None)) )
# la file
une_file = []
# appel de la fonction
parcours_en_largeur(mon_arbre, une_file)
Partie 2: implémentation d'un arbre sous forme d'un dictionnaire
Il est également possible de coder un arbre avec la structure dictionnaire étudiée en première. Voici une fonction qui renvoie un dictionnaire qui représente le noeud d'un arbre:
def noeud(nom, fg = None, fd = None) :
return {'racine': nom, 'fg' : fg, 'fd': fd}
# création d'un noeud qui contient la valeur 2
k = noeud(2) # k = { 'racine':2, 'fg' : None, 'fd': None }
# visite du noeud:
print( k['racine']) # affichera 2
# Ajout d'un nœud parent m au nœud k
m = noeud(3, k, None) # m = { 'racine':3, 'fg' : { 'racine':2, 'fg' : None, 'fd': None }, 'fd': None }
Question 2.1
Compléter l'exemple ci-dessus pour obtenir l'arbre ci-dessous:
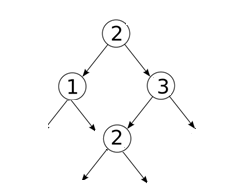
Question 2.2
Tester votre code en mesurant la taille de votre arbre avec le code ci-dessous:
def taille(arbre):
""" nombre de noeuds de l'arbre"""
if arbre is None:
return 0
else:
return 1 + taille(arbre['fg']) + taille(arbre['fd'])
Question 2.3
En vous inspirant de la mesure de la taille ci-dessus et de l'implémentation objet de la mesure de la hauteur vu en cours: écrire le code qui permet de mesurer la hauteur d'un arbre conçu avec un dictionnaire.
Partie 3: arbre de recherche ( ABR)
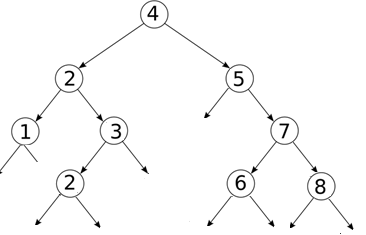
Question 3.1
Quelle propriété possède un ABR que l'on ne retrouve pas sur l'arbre binaire étudié en partie 1?
Question 3.2
Quelle est la taille de cet arbre? Quel est sa hauteur?
Citer le nombre de feuilles de cet arbre.
Question 3.3
Coder cet arbre en utilisant un dictionnaire pour chaque nœud de l'arbre.
Question 3.4: appartenance à un arbre
Écrire une fonction qui permette de déterminer si un nombre appartient ou pas à l'arbre.
Question 3.5: ajout d'une valeur dans un ABR
Ecrire une fonction qui permette d'ajouter un nombre à l'arbre en respectant la propriété d'un ABR.
Tester ce code en ajoutant la valeur 5, redessiner l'arbre avec le nœud qui porte la valeur 5.
Projet
Voir la partie projet des activités ( encadré ci-dessous) :

Créé avec HelpNDoc Personal Edition: Produire des livres Kindle gratuitement